南京市觅秀街小学六年级数学备课组3月份活动

(2023-2024学年度第二学期)

一、集体备课主题

苏教版小学数学六年级上册第三单元。

二、集体备课时间和地点

   2023年3月12日，2号楼四层西办公室。

三、集体备课的主要内容

学生分析：学生经过五年半系统的数学学习，掌握了较为完整的数学知识。大部分学生对于基础知识、基本技能的掌握比较扎实，学习态度端正，目的明确，上课专心听讲，遇到不懂的问题能主动问老师；但是还有小部分学生存在着一些问题：基础比较差，对基础知识、概念、理念缺乏深刻理解，缺少主动学习的意识和习惯，作业的正确率低。故本学期的重点抓好基础知识教学的同时，要加强后进生的学习习惯的培养，力求使他们乐学，愿学，整体学习成绩有一个新的提高。

教材分析：这册教材包括下面内容：扇形统计图、圆柱和圆锥、解决问题的策略、比例、确定位置、正比例和反比例以及小学六年来所学数学内容的总复习。本册教材的这些内容是在前几册的基础上按照完成小学数学的全部教学任务安排的，着重使学生认识一些常见的立体图形，掌握它们的体积等计算方法，进一步发展空间观念；进一步形成统计的观念，掌握用扇形统计图表示数据整理结果的方法，提高依据统计数据的分析、预测、判断能力；理解比例、正比例、反比例的概念，加深认识一些常见的数量关系，会用比例知识解答比较容易的应用题。然后把小学数学的主要内容加以系统的整理和复习，巩固所学的数学知识，使学生能够综合运用所学的数学知识解决比较简单的实际问题；结合新的教学内容与系统的整理和复习，进一步发展思维能力，培养思维品质，进行思想品德教育。

四、集体备课的具体要求

 三定：定集体备课课题，定主讲人，定上课人。

 四统一：统一教学目的，统一教学重点、难点，统一课时分配和进度，统一作业布置。

 五备：备学生、备教材、备教学手段、备方法、备练习。

 五点：重点、难点、知识点、能力点、教育点。

 两法：教师的教法和学生的学法。

 两题：课堂练习题和课后作业题。

 时间：每次备课不低于40分钟。

 纪律：所有六年级数学教师均需参加备课组活动。不得迟到、早退。集体备课期间，参加集体备课的教师要认真履行职责，积极发表自己的见解，不做与集体备课无关的事，保证集体备课的质量。

五、集体备课的实施程序

1、集体备课由备课组长具体主持集体备课活动，由备课组长负责具体实施。

2、集体备课的基本程序是：主备人备课→集体备课→主备人修改→备课组长定稿→审核→上课→教学反馈。

3、主讲人在集体备课前要深入钻研教材和大纲，反复阅读教学参考书及有关资料。集体备课时详细介绍所备课时在单元的地位及前后联系，课时教学目的，三维教学目标，教材重点难点，突出重点和突破难点的方法，作业与练习配备，教学方法的设想等。

4、年级每位教师要积极参与集体备课活动，各抒己见，充分讨论，统一认识，实行教学上的“五统一”，同时提出改进教学方法的建议。集体备课时，除主讲人做主题发言外，其他教师也要积极参与，发表自己的教学设想并阐述理论依据，经过“争鸣”，形成比较一致的意见和实施教案。活动结束后，备课组长要认真做好活动记录，以备学校领导及教务处检查。

5、信息反馈。下一次集中时，把根据备课提纲实施时反映出来的重点问题提出来，供以后借鉴。

六、活动总结

活动后及时反思总结，注重活动资料的收集与整理。

解决问题的策略。(教材第27~29页)

1. 指导学生学会用转化、列表、假设等策略解决生活中的实际问题。

2. 通过运用这些策略解决问题,提高学生解决问题的能力。

重点:指导学生学会用转化、列表、假设等策略解决生活中的实际问题。

难点:提高学生解决问题的能力。

课件。

师:同学们,回想一下在以前的学习中,有没有运用转化策略解决过问题呢?

学生可能回忆并列举出:平行四边形面积、三角形面积、梯形面积、圆形面积公式的推导过程,圆柱体积公式的推导过程。老师适时课件或学具演示,并在黑板上将转化关系用图示表示出来。

师:转化策略曾经帮助我们解决过这么多新问题,像这样的例子还有很多,你们每个人手里都有一组题,动笔算算,体会哪里运用了转化策略。有发现,可以和组内的同学交流一下。

四人小组内每个学生的题纸各不相同,学生独立计算、观察,体会到转化后,四人小组进行交流。

师:举个例子说说你的发现。

学生可能举例:

·计算分数除法是把除法转化成乘法。

·计算小数除法是把小数除法转化成除数是整数的除法。

·计算异分母分数加法是把异分母分数加法转化成同分母分数加法。

·计算83+83+83+83+83是把相同加数的和转化成乘法。

……

师:这里都用了转化策略,有什么共同地方?

引导学生观察并思考,体会到转化的实质——转化前和转化后计算结果不变。

小结:这么多地方用到转化的策略,说说你有什么体会?

学生可能体会到:转化策略应用很广泛;转化策略能解决新问题;转化策略能把复杂的问题变简单。

师:转化是常见的解决问题的策略之一,解决问题的策略还有很多要具体问题具体分析。

【设计意图:引导学生体会转化的策略,为下面探究解决问题的策略做准备】

1. 教学例1。

师:请看下面的问题,分析题中的数量关系,说说准备怎样解答,跟小组同学讨论一下。(课件出示:教材第27页例1)

学生进行小组活动,教师巡视了解情况。

师:说说你们的讨论情况吧!

学生可能会说:

·通过画图,可以看出男生人数有2份,女生人数有3份,已知女生有21人,所以男生人数是21×=14(人)。

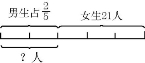
·还可以根据分数与比的关系,把“男生人数占总人数的”转化成男、女生人数的比是2:3,这样就转化成一道按比例分配的问题。所以男生人数是21×=14(人)。

·还可以直接按分数问题来解决,男生人数占总人数的,所以女生占总人数的1-=,已知女生有21人,总人数是21÷=35(人),男生人数是35×=14(人)。

师:解决上面的问题,你选择了什么策略?是怎样想的?

生1:选择画图的策略,画图能使数量关系更直观,更清楚。

生2:把分数转化成比,更容易理解数量之间的关系。

生3:选择按分数问题直接解答,关键就是找准单位“1”,以及数量之间的对应关系。

2. 教学例2。

师:解决下面的问题,你准备选择什么策略?试一试。(课件出示:教材第28页例2)

学生尝试用自己选择的策略解决问题;教师巡视了解情况,发现学生存在的问题,及时指导。

组织学生交流想法:

·我们可以用画图的策略解决问题。(如下所示)

先画10只大船,每只大船坐5人,这样就坐50人;实际全班只有42人,就多出了8人。这是因为,每只小船只坐3人,比每只大船少2人,如果去掉多出的8人,就需要从8÷2=4只大船上去,这样这4只船每只上面坐3人,所以就是4只小船,6只大船。

·我们还可以用列表的方法进行有序列举,从9只大船和1只小船开始。

 由表中数据可以知道,需要6只大船和4只小船。

·我们也可以用假设法解决问题。假设大船和小船的只数同样多,再根据总人数调整。

 由表中数据可以知道,需要6只大船和4只小船。

师:选择你喜欢的方法解答并检验,再与同学交流你的解题策略。

学生进行解答、检验并交流;教师巡视,个别指导有困难的情况。

师:回顾解决问题的过程,你有什么体会?

生1:画图、列举、先假设再调整都是解决问题的有效策略。

生2:分析和解决同一个问题,可以用不同的策略。

生3:要学会根据具体问题灵活选择策略。

【设计意图:通过唤醒学生的“解决问题策略”的已有经验,引入综合运用“转化”“画图”“列表”等策略解决问题的学习,做好教学的衔接与迁移,可以激发学生的学习兴趣】

师:用转化的策略解决了这么多问题,说说你有哪些收获和体会?

学生自由交流各自的收获体会。

解决问题的策略

新问题已经解决的问

1.教学本部分要强调独立进行,让学生在直观图形的启发下,独立进行转化。

2.通过唤醒学生的“解决问题策略”的已有经验,引入“转化”策略的学习,做好教学的衔接与迁移,可以激发学生的学习兴趣。